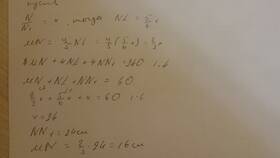Параллелепипед - это трехмерная геометрическая фигура с 12 ребрами. Для вычисления суммарной длины всех ребер необходимо знать основные параметры фигуры. Рассмотрим различные методы расчета.
Содержание
Основные свойства параллелепипеда
| Элемент | Количество |
| Ребра | 12 (по 4 равных каждого направления) |
| Грани | 6 прямоугольников |
| Вершины | 8 |
Формула для расчета суммы ребер
Сумма длин всех ребер (P) = 4 × (a + b + c)
- a - длина первого измерения
- b - длина второго измерения
- c - длина третьего измерения
Пошаговый алгоритм расчета
- Измерьте длину (a), ширину (b) и высоту (c) параллелепипеда
- Убедитесь, что все измерения в одинаковых единицах
- Сложите три измерения: a + b + c
- Умножьте полученную сумму на 4
- Результат - общая длина всех ребер параллелепипеда
Пример расчета
| Параметры | Значения |
| Длина (a) | 5 см |
| Ширина (b) | 3 см |
| Высота (c) | 2 см |
| Расчет | 4 × (5 + 3 + 2) = 40 см |
Частные случаи
Для куба (частный случай параллелепипеда)
Все ребра равны: P = 12 × a
Для прямоугольного параллелепипеда
- Формула остается стандартной: P = 4(a + b + c)
- Все углы прямые
- Ребра перпендикулярны друг другу
Практическое применение
- Расчет материала для каркаса
- Определение длины ребер при изготовлении упаковки
- Вычисление общей длины сварных швов
- Проектирование строительных конструкций
Ошибки при расчетах
| Ошибка | Как избежать |
| Разные единицы измерения | Привести все значения к одной системе |
| Учет не всех ребер | Помнить, что ребер 12 (4 набора по 3) |
| Путаница с площадью поверхности | Не смешивать расчет ребер и площади |
Вычисление суммы длин всех ребер параллелепипеда - простая задача, если знать основные параметры фигуры и правильную формулу. Этот расчет часто применяется в инженерии, строительстве и производстве.